Perhaps the problem I’ll touch on is such that firms will avoid reporting gross- and net-of-fee returns. Hopefully not.
A new GIPS(R) (Global Investment Performance Standards) verification client reached out with a problem. One of their clients subtracted their 12-month net-of-fee return from their gross-of-fee return and discovered that their result (1.28%) differed considerably from the annual fee (1.10%). As a result, the client was no doubt feeling a bit agog, anxious, baffled, befuddled, concerned, confused, disturbed, flummoxed, incredulous, irritated, morose, nervous, perplexed, skeptical, stressed, troubled, uncertain, and perhaps a host of other not very pleasant or positive emotions.
I have touched on this topic before; for example, here! But since that post is almost five years old, I thought a “redo” was in order, especially given this recent query.
Advisory fee challenge: what’s the problem?
There is really quite a simple one-word answer to this: compounding. Returns compound at different rates. If we have positive returns, then the gross-of-fee will always grow more quickly than the net, because they’re higher. (Okay, I’m ignoring those few occasions where net-of-fee can actually be higher than gross, which would be an exception to this rule). And, the higher the return, the quicker they compound.
To demonstrate this I created several scenarios where each month has the same return (0%, 1%, 3%, 5%, and -5%). The annual fee is 1.10%, and we take the fee out each month, and calculate monthly gross- and net-of-fee returns. The only time that the difference between the annual gross- and net-of-fee returns is close to the annual fee is when the return is 0.00% for all 12 months. As the returns increase, the differences between these values increase. The following graphic shows this for the 1%, 3%, and 5% scenarios:
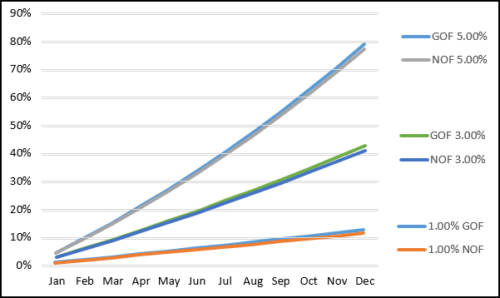 As you can see, the 5% return compounds much quicker than the 3%, which in turn compounds more quickly than the 1%. While the graphic doesn’t show the difference between gross- and net-of-fee returns very well, these differences are easily derived.
As you can see, the 5% return compounds much quicker than the 3%, which in turn compounds more quickly than the 1%. While the graphic doesn’t show the difference between gross- and net-of-fee returns very well, these differences are easily derived.
More to come on the advisory fee issue
This month’s newsletter will build upon this email, to include the details on the results for the various scenarios I reference above.
If you have an idea how to make this clearer, please chime in!
