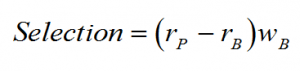I think this might be a record for blog post titles, but I came up with the second part, first, which is at the heart of the matter, and then the first came to me later, which adds some color to it.

Dealing With Off Benchmark Bets

What IS an “off benchmark bet”? It’s when a portfolio manager elects to invest in something that isn’t in the benchmark. This happens ALL OF THE TIME! Think cash: benchmarks rarely include cash (unless it’s a blended benchmark); and so, the manager has part of his/her portfolio in cash, but the benchmark is void; how do we handle this? But it’s not just cash; managers often invest in different sectors or asset classes that the benchmark isn’t in. Dealing with this situation can be a bit tricky.

If you use one of the standard models (e.g., Brinson-Fachler) and have a portfolio that is somewhere that the benchmark isn’t, unless you make adjustments to the model you’ll likely get some weird results. This is a topic that’s taken up in the revised CIPM program, and one worthy of comment here.

During a recent Performance Measurement Think Tank webinar, John Simpson, CIPM provided a very detailed explanation of the options available. I will briefly touch on them here, and then explain why they’re misleading.

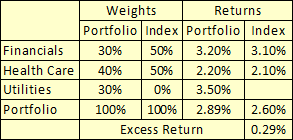
Our Off Benchmark Bets Portfolio

Let’s use this  portfolio for our example.

This is really a simple example, but it should make our journey to understanding the process an easy one. The benchmark is only in two sectors, while the portfolio is in a third. The benchmark is void in Utilities, so we see that its weight is 0%, which makes sense, since it has no securities in this sector. Its return is blank, meaning “null.” While this isn’t the same as zero, it is often treated the same way.

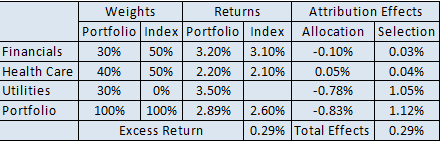
Base Case: Off Benchmark Bets – Do Nothing

Let’s see what happens when we run Brinson-Fachler as it comes, out of the box, with no adjustments:

Our allocation effect is pummeled, with a -78 basis point score; but does this make sense, since we allocated to such a great performing sector? Oh, wait a minute … the benchmark has a null (zero) return, which is below its overall return (2.60%), so we’re penalized. But, we at least did a great job of stock picking relative to the benchmark, but the benchmark doesn’t have any securities, so does this make sense?

This subject typically comes up in our Performance Attribution course, and I generally suggest that the results be totaled and shown under allocation. But, there are three more sophisticated ways to tackle this.

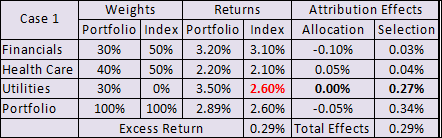
Off Benchmark Bets – Case #1

As John explained, in this case the portfolio manager has “Bottom-Upped” the Utilities sector, hence the adaptation to the model is to use the overall benchmark return as its return. The result will be that the value added is measured as “Selection.” And so, let’s see our results:

As expected, by using the index return for the utilities sector, our allocation effect goes to zero, and  our selection gets everything. And since the portfolio outperformed, we get the kind of result we expected.

How often this option would apply seems to be a question for me, but there no doubt are occasions. Now, we’ll move to:

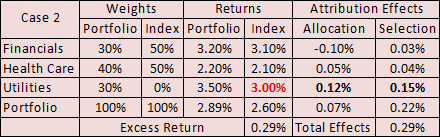
Off Benchmark Bets – Case #2

As John explained, in this scenario the portfolio manager has “Top-Downed” the Utilities sector, hence the change we make to the model is to use a proxy for the sector’s benchmark return. The value added is thus measured as Allocation and “Selection.”

We went to a different index that happened to have a Utilities sector, and brought that return across. Since we picked better securities, we get a positive selection effect; and, since the proxy’s return (3.00%) was higher than the benchmark’s (2.60%), our decision to allocate more there than the benchmark, we get a positive allocation effect. Hurrah! As expected. Finally, we look at:

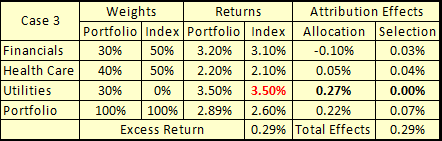
Off Benchmark Bets – Case #3

John explained that with this final approach, the portfolio manager has added assets of a class unlike other benchmark assets, hence the adaptation is to use the portfolio’s sector’s return for the benchmark.  The value added is measured only as allocation.

This is essentially what we recommend in our class: put everything into allocation. While some prefer option #2 (to use a proxy), I’m not a fan because its selection can be arbitrary; also, we’re not investing against a different index. While I understand the rationale (did the manager pick good stocks in this sector), I’m still not a big fan. But, we’ll put that aside, the really important point is:

This approach to off benchmark bets is misleading

The actual selection effect, in each of these three cases is (drum roll, please) …

0.00%

Yes, you read it correctly … ZERO PERCENT!

Why? Because the formula for the selection effect is:

Since the benchmark’s weight is zero, regardless of what we substitute for the benchmark’s utility sector return, selection HAS TO BE ZERO!

But if this is true, WHAT is the source of the values that clearly appear in cases #1 and #2?

The Interaction Effect

Space doesn’t allow me to go into this further, but this WILL be a topic in this month’s newsletter (and I’ll probably use the same title, since I like it so much!).

In the meantime, feel free to chime in. I suspect that at least two of my esteemed colleagues, who both individually and collectively disdain the interaction effect, will offer their views.

By the way, want to learn more about our Performance Measurement Think Tank? Go here! You’ll learn how you can gain access to performance measurement experts on a regular basis.