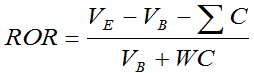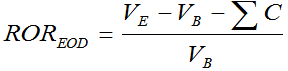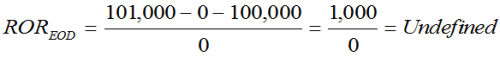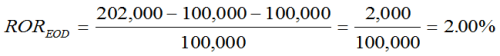One of the critically important decisions when it comes to calculating rates of return is how to handle cash flows. At a minimum, we need to contend with its timing. This is the first in a three-part series dedicated to this topic. And today, we’ll deal with:

End-of-Day Cash Flows

End-of-day cash flows means that we’re treating all cash flows as if they took place at the end of the day. For this series we’ll deal with daily treatment of cash flows, although similar arguments would apply to monthly.

It’s probably best to consider what our formula looks like when we deal with end-of-day cash flows; for our purposes, we’ll use Modified Dietz:

Quickly, our numerator represents what we earned during the period: ending value minus beginning value minus the sum of the cash flows. The denominator is the “base” upon which we judge how well we did: the beginning value plus the weighted cash flows. For daily performance our weight can be zero, for end-of-day cash flows or one, for beginning-of-day cash flows [for the purpose of this discussion, we’ll avoid the idea of employing fractions (e.g., 0.5 for mid-day) weights].

Modified Dietz for end-of-day cash flows

Since we’re dealing with end-of-day cash flows, our weight will be zero, and our formula can be reduced to:

Our return is based therefore upon our gain relative to what we began with: any cash flows that may have occurred will have no basis in evaluating our return, only our gain or loss shown in the numerator.

Two Problems with end-of-day cash flows

End-of-day cash flows have two significant problems, the first has to do with what occurs on the first day of investing. When an investor begins, they start with a cash flow, meaning on that day there is no beginning of day value.  This topic was presented by Mary Cait McCarthy, and discussed at this month’s PMAR Europe in London and Performance Measurement Forum meeting in Dubrovnik, Croatia.

Consider a very simple example:

• We begin with a cash flow of $100,000
• At the end of the day the portfolio’s value is $101,000.

What’s our return? Well, using the above formula and substituting our values we get:

Because our beginning value is zero, our denominator is zero, and the result is considered “undefined,” meaning there is no viable answer.

Firms that employ end-of-day treatment are typically aware of this problem and will either (a) adjust their formula, by treating, for this day only, the cash flow as a start-of-day event, or by avoiding the first day altogether, and starting performance with “day 2.” Alternatively, they may force (i.e., override) the timing of the flow itself treating it as if it had occurred the prior day. Any of  these approaches will work around this problem. I, for one, prefer consistency in employment of cash flows, and would recommend an alternative approach, which we’ll deal with in Part III.

The second problem with end-of-day cash flows has to do with gains (or losses) received on contributions made during the day, which are attributed solely to what the portfolio started with (since the flow won’t be recognized until the next day).

Consider the following:

• Starting value = $100,000
• Cash flow = $100,000
• Gains on both during the day = $1,000, meaning total gain = $2,000

What will the return be?

While the initial value of $100,000 did earn $1,000 during the day, the other $1,000 came from the cash flow; however, since we aren’t taking it into consideration, the entire gain ($2,000) is attributed to the starting value, meaning our return is inflated.

Unfortunately, this problem is one that is quite endemic to the end-of-day cash flows approach, and one that can cause significant problems, especially with large cash flows during volatile markets.

Parts II and III in this series will be posted shortly. As always, we appreciate your thoughts and comments. Thanks!

Note that this topic is also addressed in detail in our Fundamentals of Performance Measurement course.