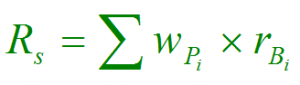Not for multi-periods, but for single periods, geometric attribution has residuals!
In a recent post about multi-period attribution, I mentioned that while it’s true that arithmetic attribution is “linking challenged,” resulting in residuals that require a smoothing factor so that the linked excess returns match the linked excess return, geometric attribution has residuals for single periods (perhaps we might call it “singe period challenged”). I thought I should explain in some detail why I state this.
Proof…comparing the formulas, mapping the factors
I’ll share with you three slides from our attribution course, which I’m in the process of revising. In the course, we discuss geometric attribution, and review the model that Carl Bacon developed: it’s a geometric equivalent of the Brinson-Fachler model.
Recall that with arithmetic models, we reconcile to the arithmetic version of excess return (simply, portfolio return (RP) minus benchmark return (RB)). Geometric reconciles to the geometric version ((RP+1)/(RB+1)-1). Returns in the models must be converted to their geometric equivalent.
Let’s first consider how we would extend the arithmetic version of Brinson-Fachler to geometric (click on the slide to enlarge it):
What I show is the conversion of the return differences from arithmetic to their geometric equivalent. As Carl explained to me, when he was developing his model the numbers didn’t work out. And so, he needed to add another factor.
Introducing, the semi-notional return
Carl introduces what he calls a “semi-notional” return (i.e., half notional, or half benchmark, where notional = benchmark):
Mathematically, it’s the “sum product” of the sectors’ portfolio weights and benchmark returns. Carl uses this return as part of his adjustment factor:
As you can see, this corrective factor is the sector’s benchmark return, plus one, divided by the portfolio’s semi-notional return, plus one.
The following shows the mapping of the attribution factors from arithmetic to geometric:
We see the use of a factor that has no corresponding expression in the arithmetic version of Brinson-Fachler. Without it, the math simply won’t work; i.e., we’ll get residuals.
Myth #2: geometric attribution doesn’t have an interaction effect
While we’re at it, let’s tackle another myth: that geometric attribution doesn’t have an interaction effect. It won’t, if, like Carl, you use the portfolio weight in the selection effect; however, if we use the benchmark weight …
If, like me, you see value in reporting the interaction effect, simply replace the portfolio weight with benchmark weight in the selection effect, and introduce the geometric version of geometric attribution … but don’t forget to include Carl’s adjustment factor!
I want to point out that on this topic, Carl is in agreement with me: geometric can have an interaction effect. He sees little (if any) benefit to interaction, which is fine; just another topic we can (and have) debate. The point here is to dispel the belief that geometric is interaction-effect-free … it isn’t!
Confession time
I taught Carl’s method as part of our attribution class for several years, but it hadn’t dawned on me that this was, in fact, an adjustment (smoothing, corrective) factor, until I reached out to Carl a few years ago, inquiring into what it was there for. That’s when he explained that it was necessary for the numbers to work. It still didn’t quite “sink in” until I reread Jose Menchero’s article on geometric attribution several months ago, and came to his explanation that geometric needs a factor to make the math work.
Summary
I believe I’ve demonstrated that, like arithmetic, geometric attribution has residuals: the only difference is that arithmetic needs it across time periods, while geometric requires it within time periods. In addition, I’ve shown how we can have an interaction effect with the geometric approach.
While I understand that many firms prefer the geometric method, it, like arithmetic, has some challenges which, like arithmetic, can be overcome.
As always, your thoughts are welcome!