In TSG’s January newsletter, I expanded upon a recent blog post where I introduced a couple graphics in an attempt to “make sense out of” negative Sharpe ratios. Two pillars of the investment performance community, Carl Bacon and Steve Campisi, chimed in with comments, which will appear in the February newsletter. In the mean time, I will take this topic a bit further, with inspiration from both gentlemen.
Would it not be useful to see how the Modigliani-Modigliani risk-adjusted measure responds to negative Sharpes? I believe so. And in truthfulness and full disclosure, I will admit to being kept awake last night thinking about this (graphing it in my head), until I got up to put the materials together.
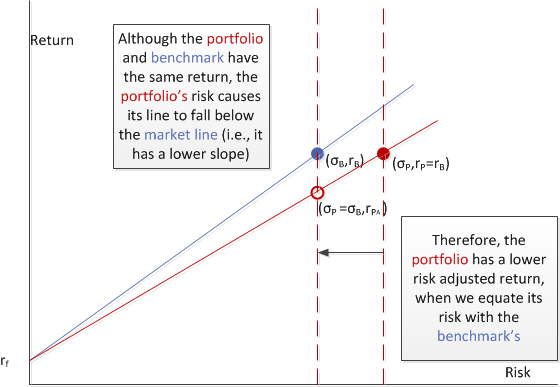
On the positive side. Let’s begin by recalling how the M-squared looks when we’re dealing with positive returns.
Recall that we first plot the benchmark (in the risk/return graph), and draw a line from the risk free rate and through it; this is the “market line.” We can next plot the portfolio, and draw a similar line. Here I show a case where the portfolio and benchmark have identical returns, but the portfolio has taken on added risk. Note that its line falls below the benchmarks, meaning it will end up with a lower M-squared value.
The fundamental step in this method is to equalize the risks, and this is done graphically here, where we shift the portfolio’s point to the left, so that it aligns with the benchmark’s risk; and, as predicted, we have a lower return.
What happens on the negative side?
I again chose a case where the portfolio has the same return as the benchmark, and where it also has taken on greater risk. But notice that it plots above the line. We again adjust the portfolio’s risk, so that it aligns with the benchmark’s, and we see that it has a higher return.
This is what people find confusing: more risk, same negative return, why not a lower Sharpe ratio (risk-adjusted return)? Do the graphics help? Perhaps in some cases, but surely not all.
That’s why I hold to the notion that we would expect that by taking on more risk, the portfolio should have a much lower return; however, it doesn’t, and thus it gets rewarded. Perhaps if we inverse the thinking a bit: the benchmark took on less risk but did equally bad (i.e., it managed to do as badly as a portfolio that took on more risk, so it somehow captured even greater negativeness than one would have anticipated.
Please let me know your thoughts. I plan to tackle this subject from a beta perspective, too!