Differential return is a risk-adjusted performance measure that many CIPM candidates have not see before, and as a result, I get a lot of questions asking what exactly is the differential return… what does it mean and how should it be interpreted. Thus, I have decided to focus on this measure in a series of posts over the next few days.
First, it is important to recognize that differential return is a rate of return. As you might guess from its name, it is an excess return (i.e., a difference in returns). More specifically, it is a risk-adjusted excess return.
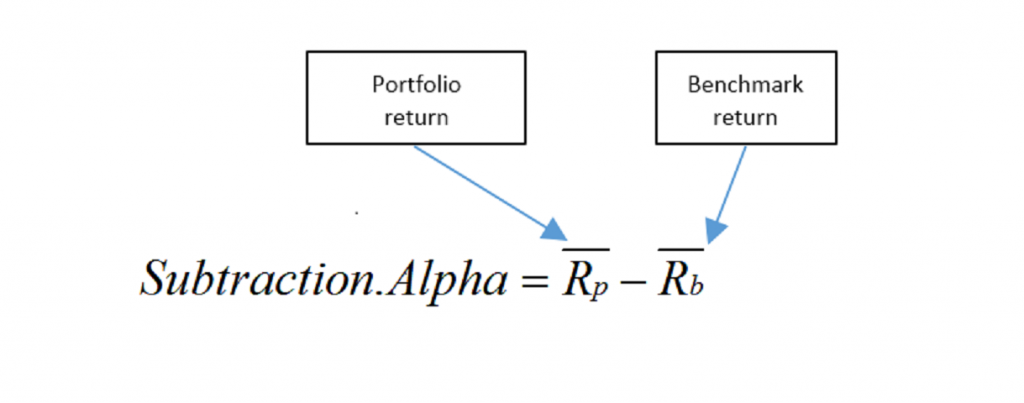
In this first post on this measure, I compare differential return to subtraction alpha. Subtraction alpha is simply the portfolio return minus the benchmark return:
Subtraction alpha is simply the portfolio return minus the benchmark return (hence the name); thus, it does not consider risk. As a result, the excess return calculated with a subtraction alpha gives the portfolio manager credit (or discredit) for the portion of returns that result from risk.
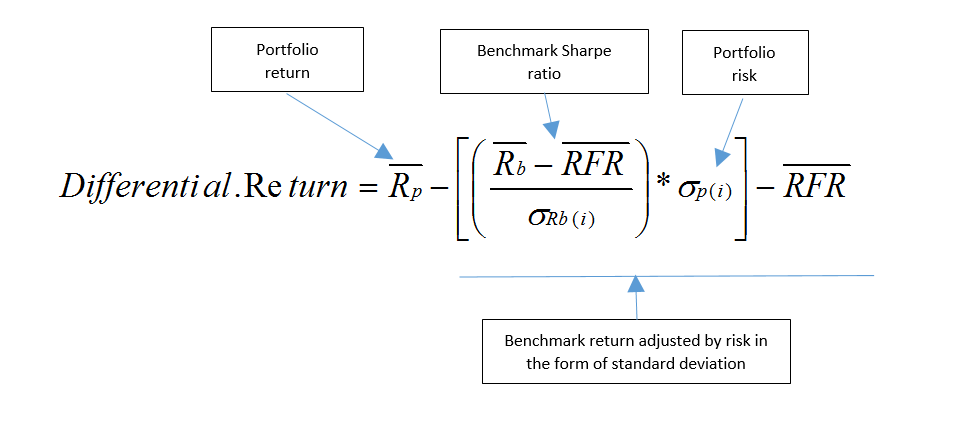
Differential return, by contrast, results in an excess return for the portfolio manager that considers risk in the form of standard deviation (the variability of past returns). Here is the formula for differential return using standard deviation:
The benchmark’s Sharpe ratio (which is the benchmark return in excess of the risk free rate, divided by the benchmark’s risk in the form of standard deviation) is multiplied by the portfolio risk to give a measure that is a rate of return (rather than the return per unit of risk, which is the basis for Sharpe ratio). The fully risk adjusted benchmark return is obtained by adding the risk free rate back in. Thus, the manager’s excess return adjusted for risk is the portfolio return minus this risk-adjusted benchmark return.
The CIPM curriculum refers to this differential return as a one-parameter performance measure (the one parameter being the Sharpe ratio, which combines return in its numerator with risk in its denominator to form a single statistic).
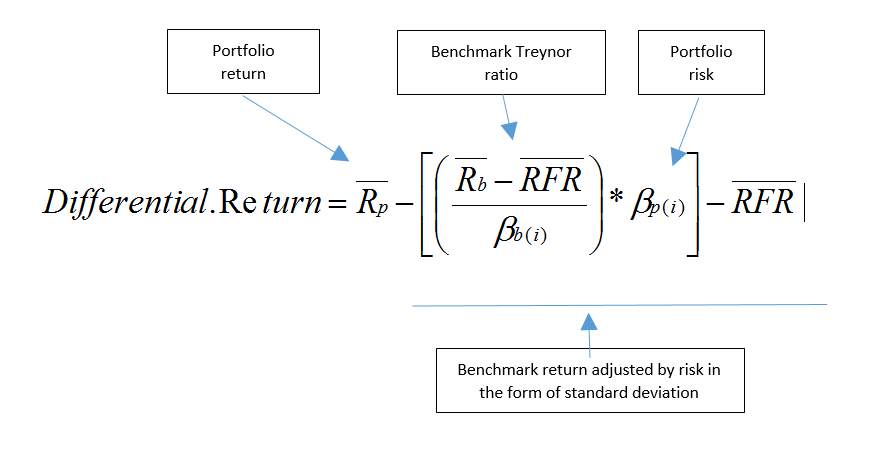
Differential return using standard deviation may be appropriate if the relevant risk measure is the variability of past returns. If the relevant risk measure is the volatility of portfolio returns compared to the market, then differential return using beta is more appropriate:
The same concepts apply… it’s just that now the Treynor ratio is used in calculation of the differential return rather than the Sharpe ratio.
Thus, differential return is a more appropriate excess return than a simple subtraction alpha.
Happy studying!