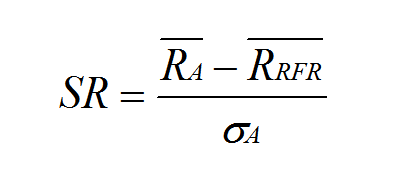Occasionally, when teaching our classes, I get a question along the lines of, “Can you explain what the Sharpe Ratio is, in 100 words or less?”
Here’s what I say (I’ll try to be concise, but it may be over 100 words…
- You could have chosen to invest without taking risk by investing in the risk-free rate (e.g., buying U.S. Treasury bills if you are an American investor… so far our government hasn’t defaulted on its debt).
- If you had taken that option, you would have earned a return that would have been very low, and positive, but very, very consistent (i.e., that return would have almost no variability to it). Remember the Sharpe ratio is appropriate if you define risk as being the variability in historical returns.
- Instead of investing risk-free, you opted to invest in portfolio A, which contains risky assets. In doing so, you accept that there will be some variability in your returns (possibly positive, possibly negative; possibly far from zero, possibly close to zero). Thus, you accept that you will have risky in your returns, which you measure using the standard deviation of historical returns.
- So, how much return are you getting, in the average period, over what the risk-free rate return earns in the average period (i.e., how much return are we getting over the risk-free rate we could have chosen to earn) in exchange for each unit of risk in the form of variable returns? That is what the Sharpe Ratio tells us.
Continuing, a bit:
- For example, a Sharpe Ratio of 0.75% tells us that for each unit of standard deviation (risk of variable portfolio returns), the portfolio is delivering 75 basis points of return per period over the risk-free rate.
- The Sharpe Ratio measures return per unit of risk. The numerator is the equity risk premium: the return earned over the risk-free rate. The denominator is risk, in the form of the variability of portfolio returns.
Happy studying!