John Simpson, CIPM and I are each (individually) teaching our Fundamentals of Performance Measurement course this week to two different clients: CalPERS in California and Florida State Board of Admin in, well, Florida, where else? One topic we take up is “multi-period performance,” which means geometric linking.

I typically ask “why don’t we just add the individual period returns together?” For example, if our returns are 1%, 2%, and 3%, why not just show 6% (the sum of the three)? The math is pretty simple, right?

The reason is compounding: returns compound. That is, returns from later periods benefit from gains/losses from prior periods. But what do we mean by that?

Well, I constructed an example to demonstrate how this works, and I think it’s helpful.

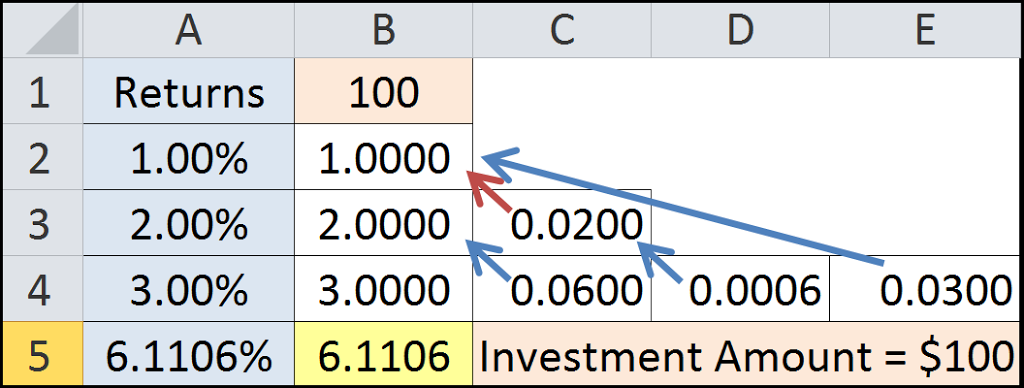
To demonstrate how compounding works, we begin with an investment of $100 (B1). Column B shows the three periods’ gains based solely on the returns applied to this amount ($1.00, $2.00, $3.00).

Compounding means that subsequent period returns are applied to all the prior period results. And so, let’s step through this.

Cell C3 shows how the second period’s return is applied to the prior period’s result (2.00% of  the $1.00 earned in the first period equals $0.0200).  And so, the second period’s 2% return not only gains from it being applied to the initial value ($100) but also the amount earned in the second period ($1.00).

Cell C4 is the third period’s return (3.00%) applied against the prior period’s gain that is earned from the initial value (i.e., it’s 3.00% × 2.00% × $100).

Cell D4’s gain comes from applying the third period’s return to the second period’s gain ($0.0200), which, in turn, came from the second period’s return (2.00%) applied to the first period’s gain (i.e., it’s 3.00% × 2.00% × 1.00% × $100).

Cell E4’s value comes from the application of the third period’s return times the gain from the first period: 3.00% × 1.00% × $100: i.e., we don’t just apply subsequent period returns to the immediate period before, but to all prior periods.

When we add these seven values together (1.00 + 2.00 + 3.00 + 0.0200 + 0.0600 + 0.0006 + 0.0300) we get 6.1106. Note that this ties in nicely with the compounded return. We earned $6.1106 for the period, which is 6.1106% of the initial value ($100).

Does this make sense? Each subsequent period’s return is applied to each prior period’s gain, as well as the starting value.

Here’s an interesting point: you get the same results, regardless of the order of the returns.

This is because of the commutative property of multiplication (i.e., A × B = B × A); since compounding involves multiplication, the rule has to apply here.

Thoughts, reactions, insights, other ideas?