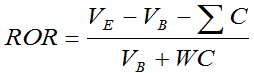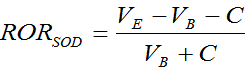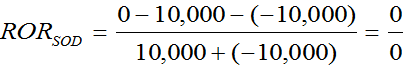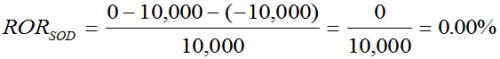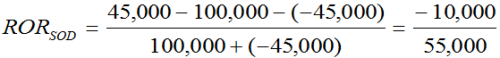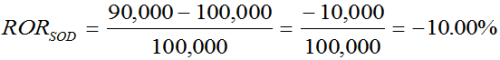As was mentioned in our previous post, one of the critically important decisions when it comes to calculating rates of return is how to handle cash flows. At a minimum, we need to contend with its timing. This is the second in a three-part series dedicated to this topic. And today, we’ll deal with:
Start-of-Day Cash Flows
Start-of-day cash flows means that we’re treating all cash flows as if they took place at the beginning of the day. Again, we’ll use daily treatment of cash flows, although similar arguments would apply to monthly.
Let’s again begin by reminding you of the Modified Dietz formula:
Modified Dietz for start-of-day cash flows
Because we’re dealing with start-of-day cash flows, our weight will be one, and our formula can be reduced to:
Our return is based therefore upon our gain or loss relative to what we began with and the entire cash flow.
Two problems with start-of-day cash flows
You might not be surprised to learn that, as with end-of-day cash flows, there are two problems with start-of-day cash flows, but in each case they’re the reverse of what we witnessed last week.
The first has to do with the last day an account exists (i.e., when a portfolio is liquidated; as opposed to the first day with start-of-day flows). Because a terminating account will often have a withdrawal equal to its beginning of day value, our denominator once again becomes zero; however, our numerator will also be zero. Please consider this example:
- Our portfolio starts the day with $10,000
- The client directs the manager to transfer the entire amount out, and so we have a withdrawal equal to this value ($10,000).
Our return:
The result (0 divided by 0) is referred to as being “indeterminate.” I.e., we are unable to determine a value, a result. This is obviously a problem.*
A “work around” is to override our normal start-of-day rule, and treat this withdrawal as an end-of-day event. By doing that, we will get the following:
The second problem deals with losses (or gains) that result from the sale of an asset and the subsequent withdrawal of the proceeds, with the overall loss (or gain) attributed what the portfolio began with, less the withdrawal amount. Let’s consider this situation:
- The portfolio holds 1,000 shares of a security valued at $100 a share, so the total start of day value is $100,000.
- Half the position (500 shares) is sold; at the time of the sale, the price per share of the stock has dropped by 10% to $90
- The proceeds of the sale ($45,000) are withdrawn. The withdrawal is treated as a start-of-day event.
- The remaining shares are valued at the same $90 price at the end of the day.
Our return is:
Let’s pause briefly: what are we seeing up to this point? Our numerator reflects our overall loss in value: our portfolio began at $100,000 and (at the time of the sale, when the price of the security was $90 per share) went to $90,000, for a drop of $10,000. This is being measured against what? Our starting value less our withdrawal: meaning, that this overall loss to the portfolio is relative to the starting portfolio value ($100,000) adjusted for the withdrawal (of $45,000), or $55,000. When we complete the math we find that the result is:
I don’t know about you, but I find this to be an exaggeration of our loss. We know that the stock price dropped by 10%; had we not sold the stock, our position for the day would have been $90,000, and the return:
It was an example such as this that first made me realize that start-of-day cash flows, just as end-of-day cash flows, can have problems.
In our Fundamentals of Performance Measurement course we discuss other examples, one in particular from an actual portfolio which resulted in a severely overstated loss.
The next part in this series will offer an alternative to the start-of-day cash flows and end-of-day cash flows approach, both of which can have some serious issues. Please feel free to offer your thoughts, insights, and perhaps even examples. Thanks!