One of the frequently debated topics in performance measurement is the value of the interaction effect.
In last week’s post, Carl Bacon, CIPM suggested that I had made a “solid case for the stupidity of interaction.” His disdain for this measure is legendary, as is that of Stephen Campisi, CFA. And when two well known industry veterans such as these agree on something, folks often will tend to ignore the other side of the argument, and believe that they surely must be correct. However, when you put the likes of Gary Brinson, CFA up against them, perhaps it would be better to put a hold on your rush to judgment.
Investment decisions by equity managers … is interaction one of them?
Top-down equity managers frequently make two distinct decisions: allocation and selection. One would expect that the allocation decision would arise first. That is, after scanning the various sectors and/or subsectors, managers predict which will perform above average and which below average. As a result of this analysis, they will tend to overweight those sectors they expect to do well, and underweight those they expect to do less well. After this is done, portfolio managers select the individual securities they wish to hold. Two decisions that we wish to analyze as part of our attribution analysis: i.e., we want to judge how each contributes to the excess return.
And even if the decisions are made in unison, would we not want to separate them in our analysis, so that we could better understand how each, distinct in itself, contributed?
Since there’s no interaction decision, there shouldn’t be an interaction effect … or should there be?
A sometimes cited argument against the interaction effect (by the arguably short sighted, pun intended) is that no one makes an interaction decision.
Quite true! There is no explicit “interaction” decision. Can’t argue with that. But that, in and of itself, is hardly justification to avoid it.
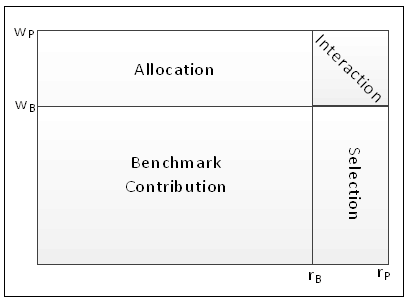
Interaction is the interaction of two decisions: allocation and selection. This graphic, which I believe Andre Mirabelli, PhD first crafted, is a good visual aid to understand what’s going on and how the effects are derived:
 There are generally three acceptable ways to handle the interaction effect in reporting:
There are generally three acceptable ways to handle the interaction effect in reporting:
- Show it by itself
- Include it with the selection effect
- Include it with the allocation effect.
Most folks who don’t like option 1 go with option 2.
What’s the problem with options 2 and 3 for dealing with the interaction effect?
In a word:
they’re arbitrary!
Just as some attribution model designers avoid residuals by assigning whatever remains in selection or some other effect, putting interaction with selection or allocation is simply a way to avoid dealing with it.
A few argue that interaction belongs with selection. But their argument is, in my view, a weak one; and one that can be discredited by analysis, thought, reflection, and the formulas themselves.
We use the benchmark weight when calculating Brinson-Fachler selection in order to avoid mixing in the allocation decision with selection, since the portfolio weight is the manager’s allocation. It’s the same reason we use the benchmark sector and overall return with allocation.
An interaction effect example to consider
Please consider the following:
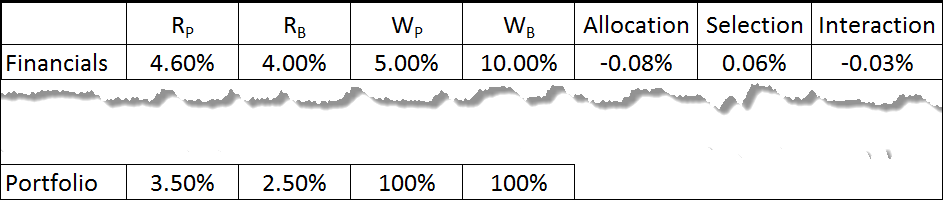
This is just a part of a portfolio, but it has the sector I wish to review. What do we see?
- The Financials’ sector’s benchmark return (4.00%) was superior to that of the overall benchmark (2.50%)
- The manager did a better job picking stocks than the benchmark (4.60% vs. 4.00%)
- The manager unwisely underweighted this good performing sector (5% vs. 10%).
Because of the poor allocation decision, we’re not surprised to see that it cost us 8 basis points. Our better selection yielded a positive 6 basis points. And the combination of these two decisions (poor allocation with good selection) yielded a poor interaction effect (-0.03%).
When folks say that explaining interaction is difficult, I suggest they look at the numbers. The negative three basis points is attributable to the poor allocation decision, combined with the good selection decision.
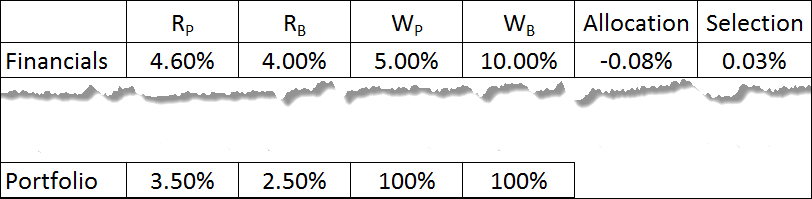
But let’s say you want to do as some suggest: combine interaction with selection, by using the portfolio weight in the selection effect. What do we get?
The good news: no interaction effect to worry about.
The bad: our selection effect has been cut in half.
Is this deserved?
How can we justify penalizing selection by – 3 bps, which resulted from a poor allocation, not selection, decision?
Perhaps the answer is, “well, there are times when selection will be rewarded by good allocation decisions.” While that may be true (that is, over time, the positive and negative effects balance out, but there’s definitely no way to guarantee this), if we’re looking for accuracy in our analysis, we shouldn’t much care about what happens at other times. For this analysis, we’re reporting a lower selection effect than we should.
If we use the portfolio weight, is it still the “selection” effect?
No; it’s more, since interaction has now been included with it. And I’m pleased when I see attribution reports that label the effect not as “Selection” but “Selection + Interaction” when the portfolio weight is substituted for benchmark weight. But it’s still, in my view, less than ideal.
And so, what’s the best way to handle the interaction effect?
While I’m quite comfortable seeing the interaction effect, I think it would be better to assign it to allocation and/or interaction, as the result of some analysis, not arbitrarily.
I wrote about this in an article for The Journal of Performance Measurement® titled “Should the Interaction Effect be Allocated? A ‘Black Box’ Approach to Interaction.” In it, I detail examples of logic that can be employed to properly assess how interaction should be assigned.
Handling the interaction effect can be likened to handling residuals
In a recent blog post, I addressed the way two different model designers handle the interaction effect that arises from using a geometric model: Carl Bacon assigns it to selection, while Jose Menchero performs additional analysis and assigns it to all effects.
As noted above, putting interaction with selection is, in my view, an arbitrary decision. Why not go the extra step and put it where it belongs? In the example above, I’d put it entirely with the allocation effect, since it’s clear that it was attributable to the underweighting decision. There are other times when it will belong entirely with selection. And other times when it should be spread between both.
In conclusion …
Okay, so you don’t want to report the interaction effect? Then don’t! But then put it where it belongs, so that your analysis is improved. I believe it best to do this analysis, and second best to show it by itself. Bringing up the rear would be to arbitrarily assign it to selection.
Have some thoughts on this? Please chime in!
Want to learn more about this subject? Attend one of our training classes, where we devote a significant amount of time to attribution. Or, start a subscription to The Journal of Performance Measurement: the industry’s primary source of research on attribution and all things related to performance and risk measurement.